今天是我們的名面上最後一天,我們要探討的是深度學習
**深度學習(Deep Learning)**無疑是其中一個最重要的領域。
從自動駕駛汽車、語音識別、推薦系統到圖像分類,深度學習正在塑造未來的數位世界。
它模仿人類大腦神經網路的結構和運作方式,使電腦能夠從大量數據中學習、推理並做出決策。
學習深度學習不僅是一扇通向未來技術的門,也是探索人工智能潛力的第一步。
這個領域不僅充滿了創新,更能解決許多現實生活中的複雜問題,讓我們的生活更智能、便捷。![]()
今天的目標是:
神經網路的誕生是多種因素共同推動的結果,既有理論上的需求,也有技術和應用層面的發展。以下是促成神經網路誕生和發展的關鍵原因:
這邊Roni想要特別補充為什麼線性不可分特別重要
馬文·明斯基(Marvin Minsky)和西摩·帕帕特(Seymour Papert)這兩位大老當初提出詳細分析了感知機的能力和局限性。他們指出了單層感知機無法解決線性不可分問題,特別是像XOR問題這樣的非線性問題。由於單層感知機的這些局限性,他們對神經網路的潛力持懷疑態度。
首先先幫大家介紹什麼是線性可分跟線性不可分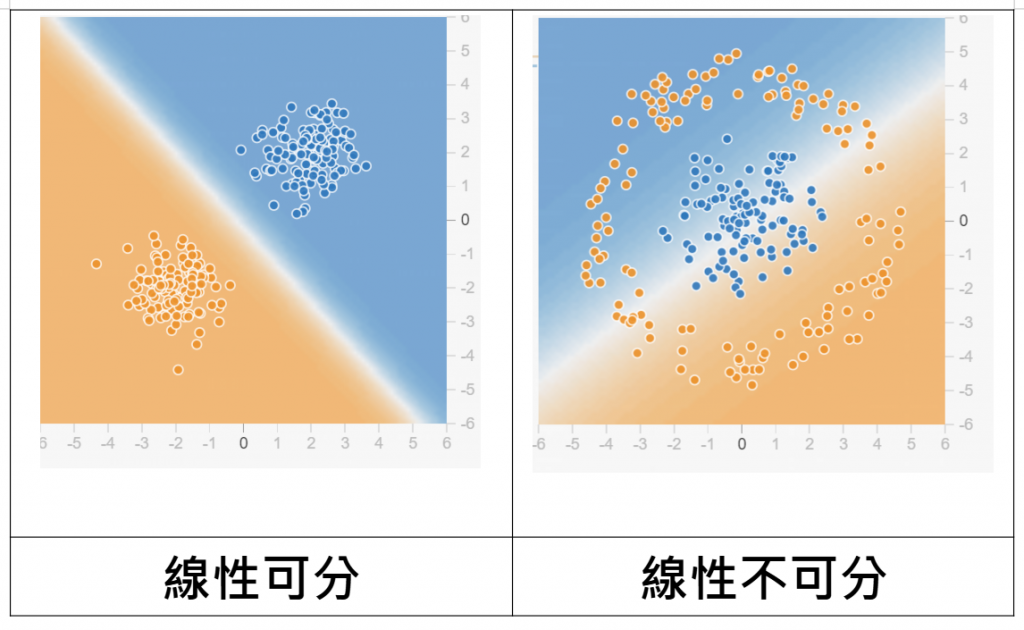
| 類別 | 定義 | 示例 | 總結 |
|---|---|---|---|
| 線性可分 | 一組數據可以用一條直線或超平面完全分開。 | 存在一條直線能夠將所有 A 類點與所有 B 類點分開。 | 可以用直線或超平面完全區分不同類別的數據。 |
| 線性不可分 | 一組數據無法用一條直線或超平面完全分開。 | XOR 問題:無法用一條直線分開 (0,0)、(1,1) 與 (0,1)、(1,0)。 | 無法用直線或超平面完全區分不同類別的數據,通常需要更複雜的模型來處理。 |
線性跟非線性的應用
| 類別 | 實際應用 | 說明 |
|---|---|---|
| 線性可分 | 信用卡欺詐檢測 | 使用交易特徵來判斷交易是否為欺詐行為,適合線性模型。 |
| 情感分析 | 判斷文本的情感傾向,某些情感特徵可能是線性可分的。 | |
| 醫療診斷 | 使用年齡、血壓等特徵來區分健康與生病的患者,適合線性模型。 | |
| 線性不可分 | 圖像識別 | 像素值特徵通常是線性不可分的,需要使用 CNN 等複雜模型。 |
| 語音識別 | 語音信號特徵通常是非線性的,需使用 RNN 或 LSTM 模型。 | |
| 自然語言處理 | 文本分類或翻譯任務中,語言的複雜性使得數據通常是線性不可分的。 |
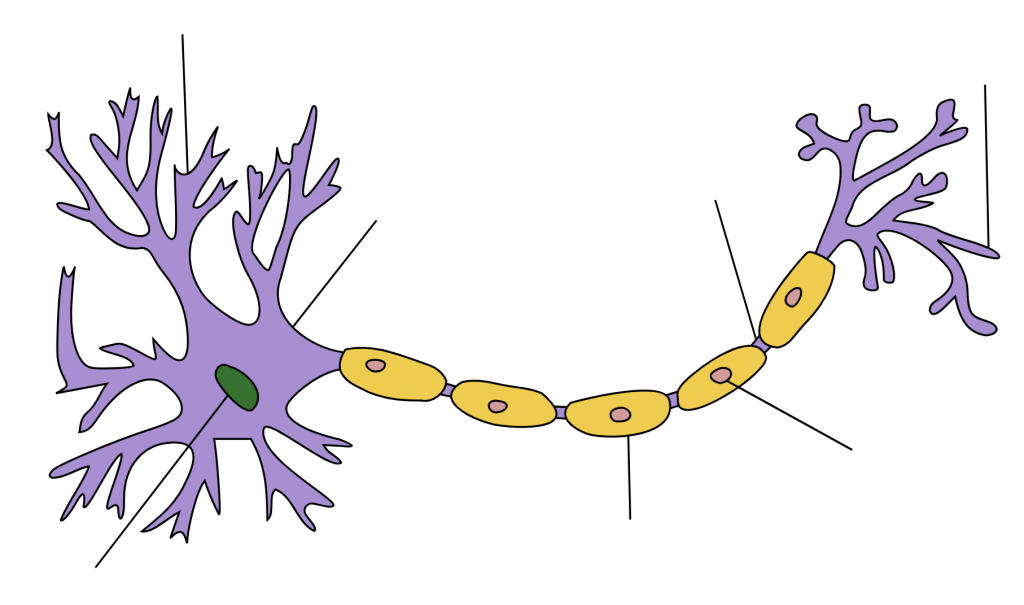
來源:https://zh.wikipedia.org/zh-tw/%E7%A5%9E%E7%B6%93%E5%85%83
人們透過神經突觸來想像神經網路的誕生。
微積分上的鏈鎖率(Chain rule)可以從神經網路的末端開始計算誤差與各權重的關係,藉此減少運算量。
尤其是近期Nivida、Meta、Google各大運算的硬體興起這個就不用說明了吧XDD
硬體提升把算法提升起來了!!![]()
這些框架也跟python脫離不了關係
這也是為啥我們會來學python XDD
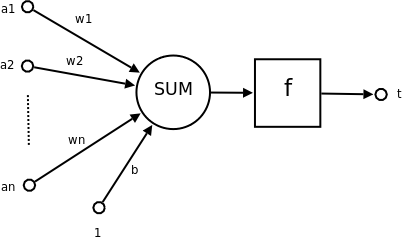
來源: https://zh.wikipedia.org/zh-tw/%E6%84%9F%E7%9F%A5%E5%99%A8
激活函數(Activation Function)在神經網路中扮演著至關重要的角色,主要用於引入非線性,這樣神經網路就能學習並處理複雜的數據特徵。如果**沒有激活函數,神經網路僅僅是簡單的線性回歸模型,無法處理非線性問題
**
簡單來說就是在數值輸出前,會先經過這個函數模型運算把值分類
| 激活函數類型 | 輸出範圍 | 優點 | 缺點 | 適用場景 |
|---|---|---|---|---|
| Sigmoid | 0 ~ 1 | - 將輸出壓縮到概率範圍 - 適合二元分類 | - 梯度消失問題 - 訓練慢 | 二元分類任務 |
| Tanh | -1 ~ 1 | - 較好的對稱性 - 與Sigmoid相比表現更好 | - 梯度消失問題 | 需要對稱數據的場景 |
| ReLU | 0 ~ ∞ | - 訓練速度快 - 減少梯度消失 | - 可能遇到神經元死亡問題 | 深層神經網路的隱藏層 |
| Leaky ReLU | -∞ ~ ∞ | - 解決ReLU神經元死亡問題 | - 仍有不穩定梯度問題 | 深層網路,避免ReLU神經元死亡 |
| Softmax | 0 ~ 1 (概率分佈) | - 將輸出轉換為概率分佈 - 適合多分類 | - 計算量較大 | 多分類問題的輸出層 |
**以ReLU vs Sigmoid **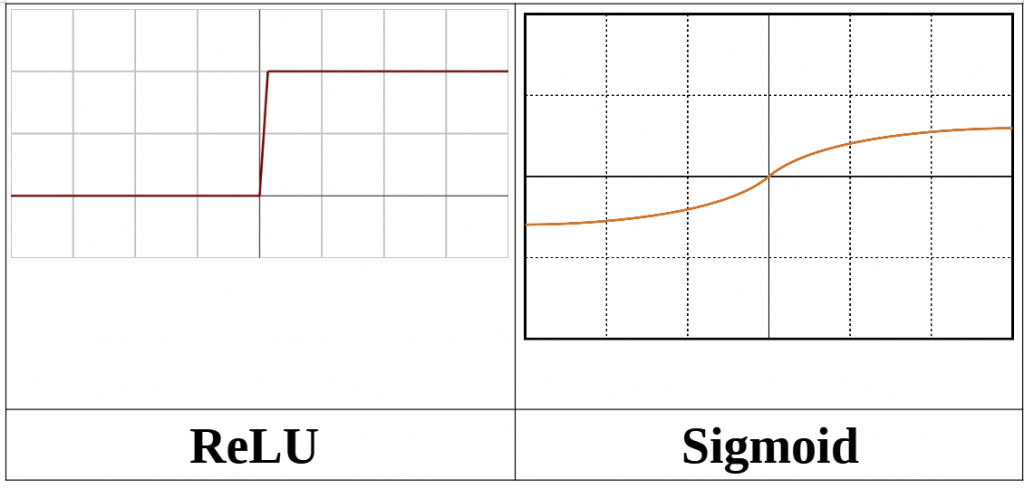
ReLU vs Sigmoid 優勢對比
| 激活函數 | 優勢 | 適用場景 |
|---|---|---|
| ReLU | - 計算簡單,訓練速度快 | 深層神經網路的隱藏層 |
| - 減少梯度消失問題,梯度不會趨於零 | 深度學習,特別是卷積神經網路 | |
| - 允許神經網路在非線性變換上有更大的靈活性 | 大型模型訓練 | |
| Sigmoid | - 輸出平滑且連續,適合用於概率估計 | 二元分類問題 |
| - 將輸出壓縮到 0~1 之間,能夠解釋為概率 | 較淺層的網路模型 | |
| - 較為穩定,不會產生劇烈的輸出波動 | 小型或簡單模型的輸出層 | |
| - 適合需要平滑輸出的場合,如一些連續數據模型 |
簡單說就是從圖形可以看到如果值直接從0跳到1比較不平滑,有點突兀
但是如果是sigmoid我們可以散步在平滑的0到1數值
這個章節很簡單,想要讓大家從excel公式中模擬model training的分解動作
| 學生 | 英文 | 數學 | 自然 | 投資報酬率 |
|---|---|---|---|---|
| A | 0.85 | 0.5 | 0.45 | 0.5 |
| B | 0.65 | 0.4 | 0.35 | 0.39 |
| C | 0.55 | 0.75 | 0.8 | 0.76 |
| D | 0.35 | 0.98 | 0.97 | 0.92 |
| E | 0.5 | 0.9 | 0.88 | 0.89 |

今天我們得到一個學生成績的總表報酬率是某家科技公司的職場滿意度的結果
也就是我們要算出這幾名學生各科分數造成的投資報酬率提升函數
這邊我要先破耿,因為我的目標就是讓自然跟數學好的學生會得到好的報酬率
先破梗的原因是讓大家有這個底子,實際上去做操作會比較有fu喔~![]()
A * w1 + B * w2 + C * w2 + B = Y
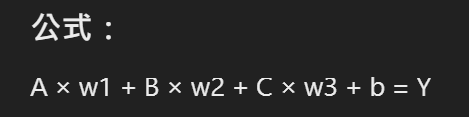
A、B、C:這些符號代表輸入變數,也就是不同的特徵或輸入值。在這個情境下,假設它們可能代表學生的科目分數(如英文、數學、自然等)。
w1、w2、w3:這些符號代表 權重(weights)。在機器學習和神經網路中,權重決定了每個輸入變數對最終輸出的影響。不同的輸入會有不同的權重,權重越大,該輸入對結果的影響就越大。
B(第二次出現的B):這裡的 B 並不是變數,而是代表 偏置項(Bias)。偏置項是一個附加的常數,它有助於調整模型的輸出,使其更靈活。偏置不受輸入影響,是一個固定值。
Y:這是 預測值(Output/Prediction),代表根據輸入變數和權重計算出的最終結果。在你的情境中,它可能是學生的 投資報酬率(或其他輸出目標)。
這個公式表示將每個科目分數(A, B, C)乘以相應的權重(w1, w2, w3),加上偏置項B,來預測某個最終結果(Y)。這類公式通常用於線性回歸或神經網路的單層結構中,來表示輸入和輸出之間的線性關係。
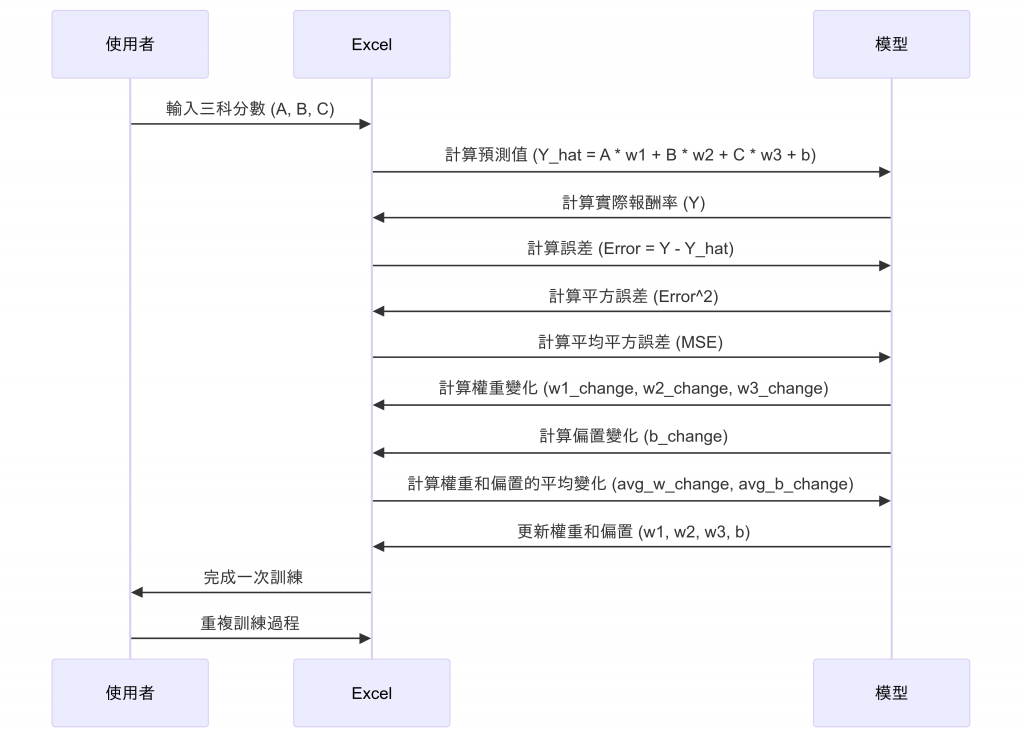
將每個科目的分數(如英文、數學、自然)乘上對應的權重 w1、w2、w3,再加上偏置 b,這會產生該學生的預測值 Y_hat(預測的投資報酬率)。

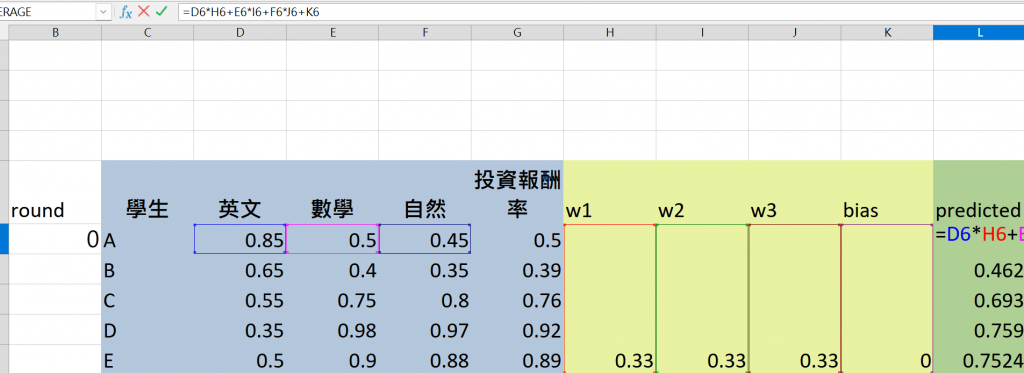
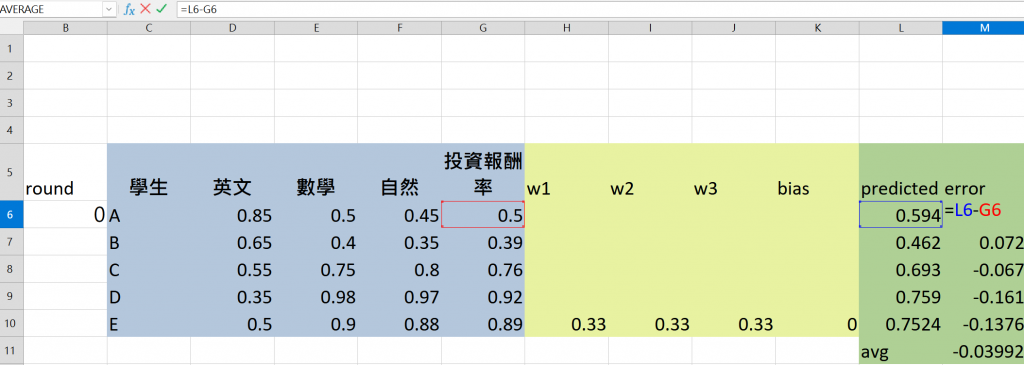
以此類推我們可以把5比學生的結果都列出來拉出所有的predicted
使用實際的投資報酬率 Y,將其減去預測值 Y_hat,以獲得該學生的誤差 Error。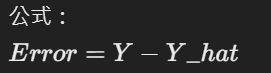
此誤差代表模型的預測與實際之間的差距。
為了讓誤差值總是為正並加速訓練,我們會將 Error 值平方,得到誤差的平方值。
這樣的轉換確保負誤差和正誤差同樣被重視,並且強調大的誤差。
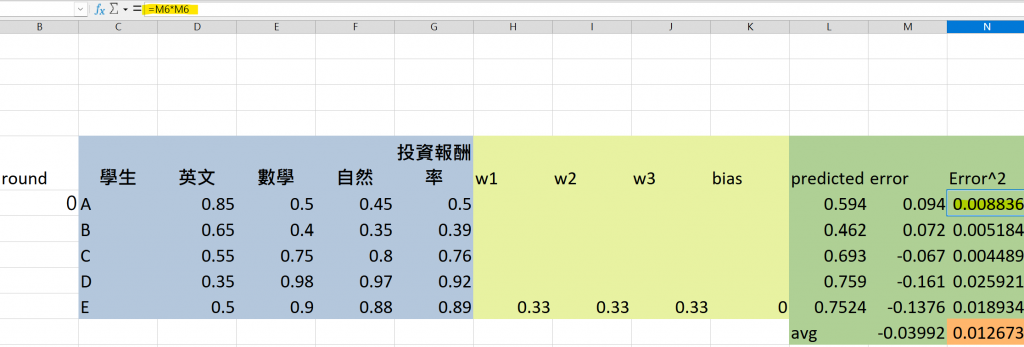
大家可以看到我上方是把error做相乘也就是平方的動作
將所有學生的誤差平方值相加,再除以數據筆數,得到平均誤差平方(MSE),這是我們用來衡量整體模型預測準確性的重要指標。
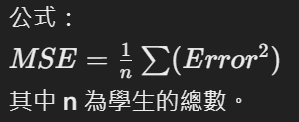
在excel中我們可以用average(第一筆:第五筆)的方式框起來計算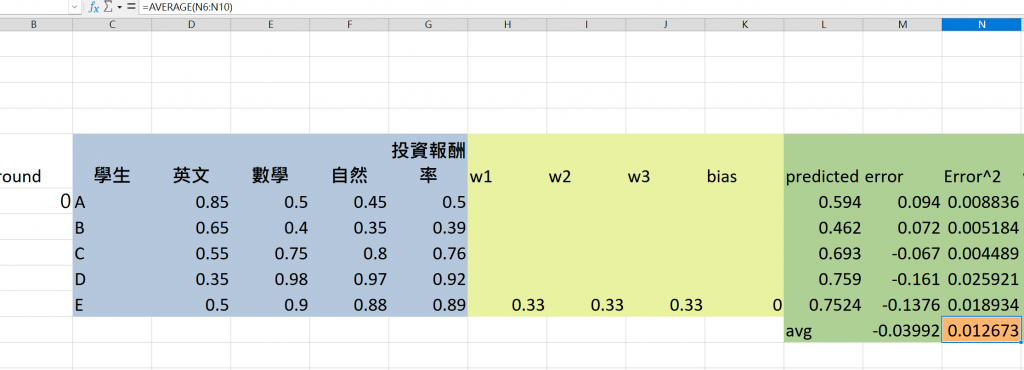
暫停思考一下
到這個地步我們就把基礎的模型建出來了
我們可以手動去調整權重跟bias來看error有沒有縮小來判斷是否調到最佳參數
但這種方法沒有達到學習跟training的目的
所以我們必須要有可以自動調整權重跟偏差值的公式
也就是說我們要把每個權重的因子做計算來算出w1,w2,w3的變化量
透過原本權重+上變化量就是我們模型的權重調整值 => 這個步驟也稱之為training

我們會根據每科的誤差乘上每科的分數來調整權重。
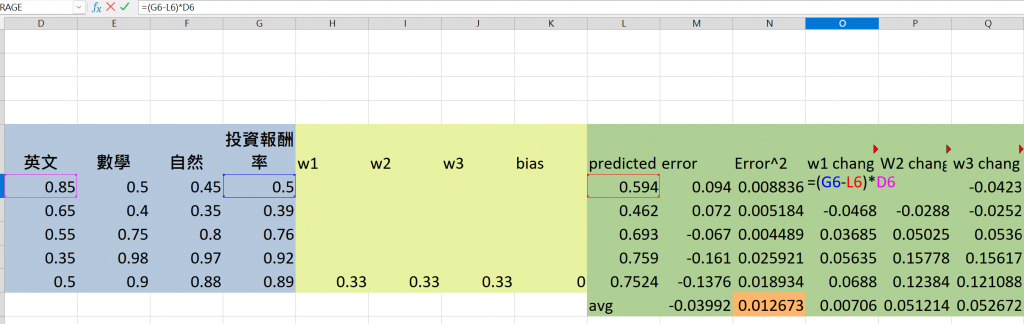
這些變化量會反映每個科目對模型預測誤差的貢獻。
w1 change來舉例就是英文的權重變化
英文的權重變化 = ( 英文權重 - 英文預測值) * 英文分數
其他的科目也以此類推
偏置變化量通過直接使用預測誤差來計算。這代表整個模型的偏差。
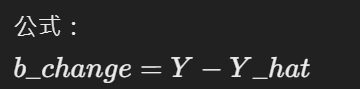
偏差比較簡單就是預測值減掉報酬率
將每個學生的權重變化和偏置變化求平均,得到每次更新時的變化量。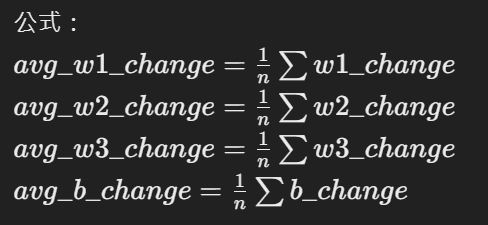
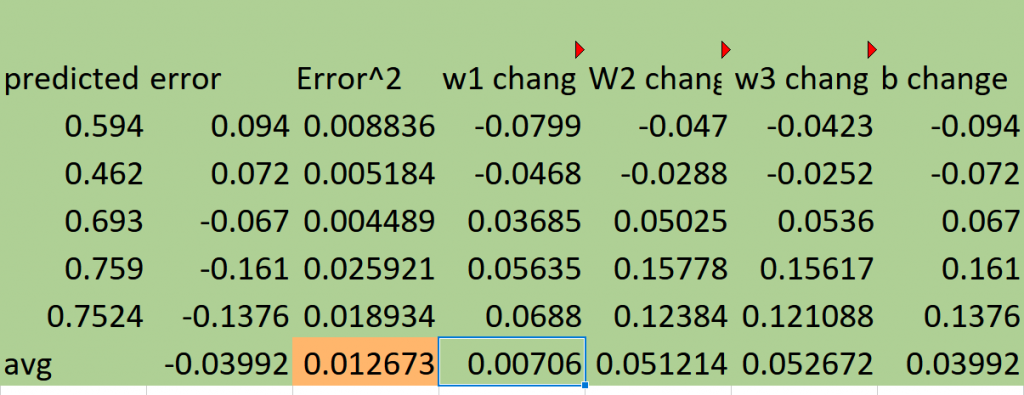
透過把原本的權重和偏置加上平均變化值來更新權重和偏置,進行第一次訓練更新。
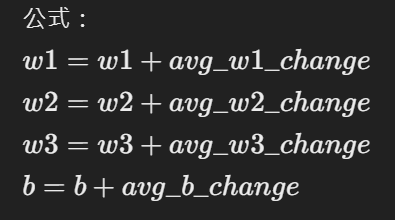
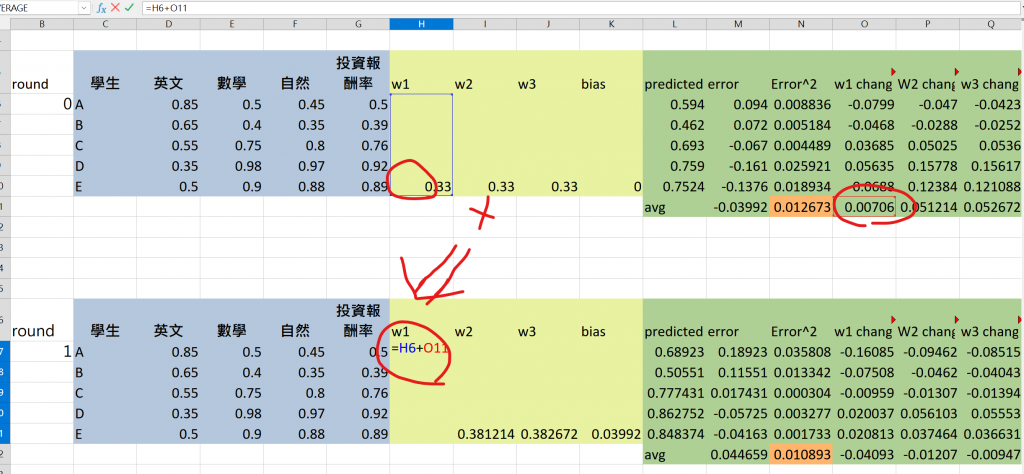
透過公式我們操作excel的步驟
就是
其他的W也以此類推
這些步驟,逐步更新權重和偏置,從而讓模型更加準確。每次訓練後,會進行多次訓練(多層訓練),使模型最終能夠更好地進行預測。
我們只要重複貼上excel的格子就可以進行training動作了
第0回
MSE = 0.012672752
第5回
MSE = 0.00295149169258037
這樣我們就學到最簡單的神經網路模型跟model training的功能了 有沒有很酷呢!!?
計算重點是
1. MSE 越小就代表方向是對的
2. training的格子要對齊,否則excel可能會抓錯格子導致公式失敗
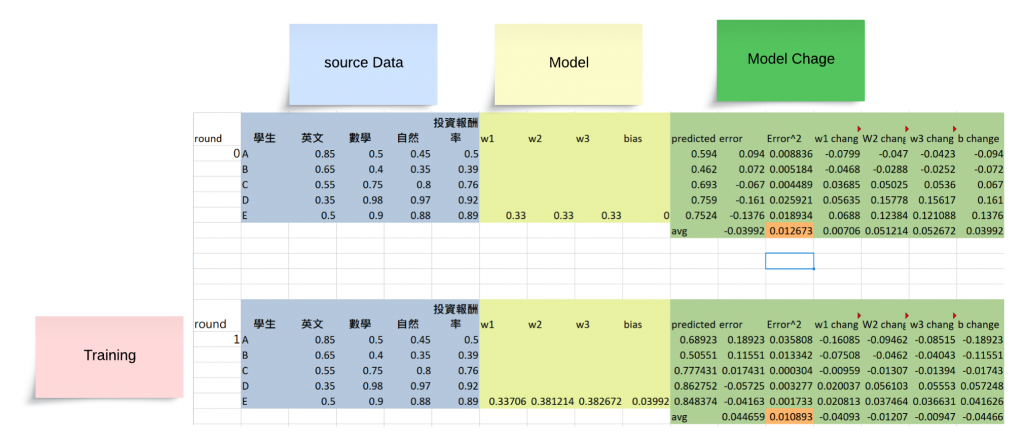
使用 Excel 訓練好的模型後,當有新的資料時,可以按照以下步驟進行簡單預測:
比如說我要預測這筆
可以得到結果如下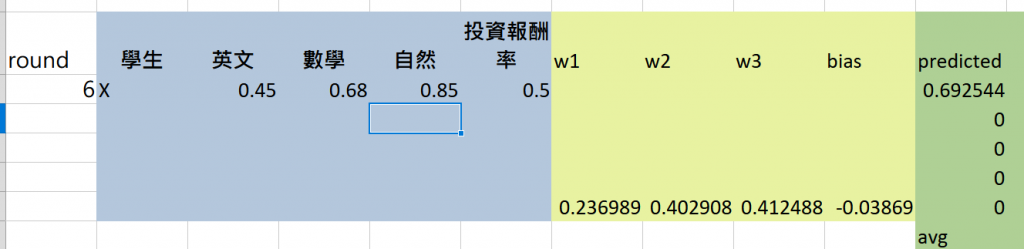
可以把其他部必要得格子刪掉比較好觀察喔
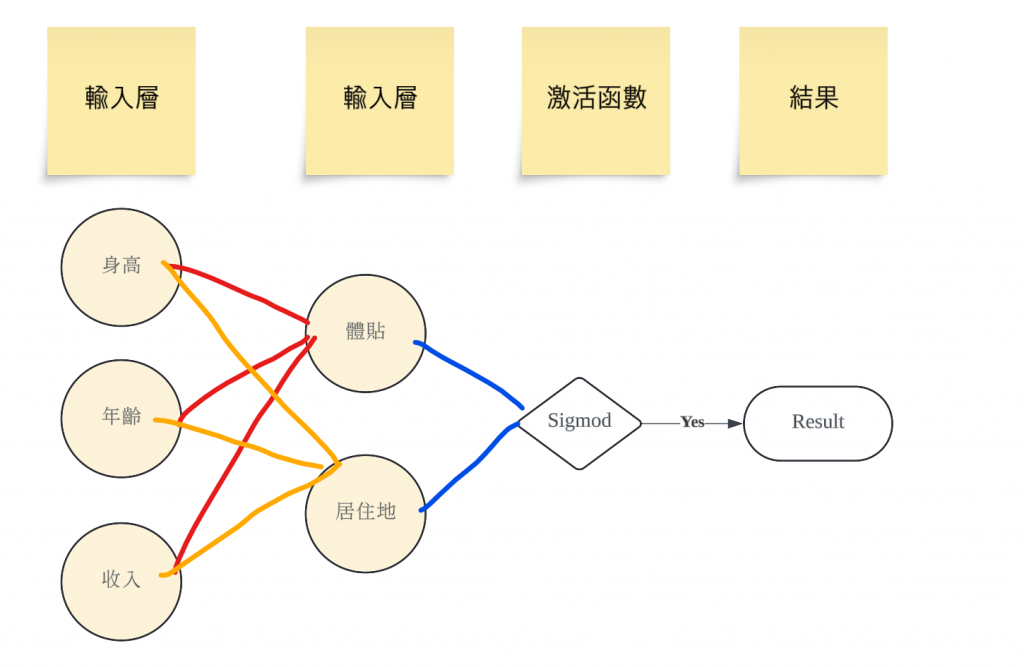
實戰來做神經網路輸出
要建立一個簡單的神經網路範例來預測「女神是否喜歡你」,您可以使用 Python 和一些流行的機器學習庫,如 TensorFlow 或 PyTorch。以下是如何設計這個神經網路的步驟,包括數據準備、模型構建和訓練。
import pandas as pd
import numpy as np
import tensorflow as tf
from sklearn.model_selection import train_test_split
# 隨機生成模擬數據
np.random.seed(42)
data = {
'height': np.random.randint(150, 200, size=100), # 身高
'age': np.random.randint(18, 40, size=100), # 年齡
'income': np.random.randint(30000, 100000, size=100), # 收入
'considerate': np.random.randint(0, 2, size=100), # 體貼 (0: 不體貼, 1: 體貼)
'distance': np.random.randint(0, 2, size=100), # 居住地遠近 (0: 遠, 1: 近)
'liked': np.random.randint(0, 2, size=100) # 女神是否喜歡 (0: 不喜歡, 1: 喜歡)
}
# 創建 DataFrame
df = pd.DataFrame(data)
# 分割特徵和標籤
X = df[['height', 'age', 'income', 'considerate', 'distance']]
y = df['liked']
# 分割訓練集和測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 建立模型
model = tf.keras.Sequential([
tf.keras.layers.Dense(5, activation='relu', input_shape=(X_train.shape[1],)), # 隱藏層
tf.keras.layers.Dense(1, activation='sigmoid') # 輸出層
])
# 編譯模型
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
# 訓練模型
model.fit(X_train, y_train, epochs=50, batch_size=10)
# 評估模型
loss, accuracy = model.evaluate(X_test, y_test)
print(f'Accuracy: {accuracy * 100:.2f}%')
# 預測新數據(例如:身高180,年齡25,收入50000,體貼1,距離1)
new_data = np.array([[180, 25, 50000, 1, 1]])
prediction = model.predict(new_data)
print(f'Predicted probability of being liked: {prediction[0][0]:.2f}')
由於套件硬體問題
我建議可以透過google colab來玩層這次實戰喔~!!![]()
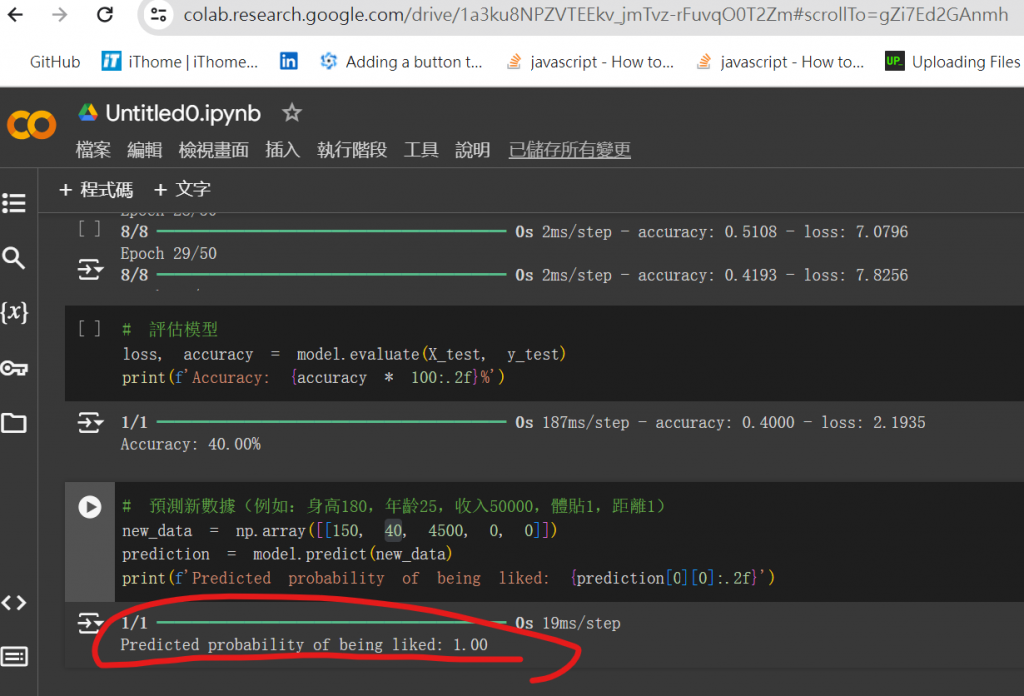
colab可以讓我們看到許多training的過程
還有一步一步呈現
是非常好用的工具喔~!!!
為什麼要學深度學習?
深度學習的核心知識
用 Excel 來模擬 Model Training
實戰來做神經網路輸出
我們完成了本次Python的專案了 ~呼
如果還有時間就更新後面學習心得吧!!!![]()
